Understanding Bias And Variance In Machine Learning
Why look at bias and variance. Errors resulting from them. Bias vs variance tradeoff.
Hey reader, welcome to the 💥 free edition 💥 of my weekly newsletter. I write about ML concepts, how to build ML products, and how to thrive at work. You can learn more about me here. Feel free to send me your questions and I’m happy to offer my thoughts. Subscribe to this newsletter to receive it in your inbox every week.
Let's say you want to build a machine learning model that to predict the likelihood of a loan default. This is very relevant to financial institutions that issue loans to large number of people. To do this, you use a labeled dataset that has the relevant details. In the machine learning domain, this comes under the supervised learning umbrella. You learn from the training dataset and use that to make a prediction on something you haven't seen before.
When you're building a model and you don't know how it would turn out, you need to run a set of experiments to figure out what works and what doesn't. If you tune the model too much to fit the training dataset exactly, it won’t generalize well when it comes to unknown data. If you let the model be too general so that it works well with unknown data, it might not detect all the underlying patterns in your training dataset.
How should we check if the training data is good enough? What issues can cause the machine learning model to be sub-optimal?
What's the problem?
When you build machine learning models, your aim is minimize the error in the model. It means that the model should be able to make accurate predictions on previously unseen data.
To reduce the errors, you need to understand where the errors can come from.
Once you know where the errors are coming from, you can attempt to minimize them.
Let’s consider the problem of loan defaults. To grow the business, financial firms have to issue loans on a large scale and recover them. Since they deal in large volumes, they need to automate this process in order to keep up.
This is where machine learning comes into play — to automate the decision of whether or not they should issue the loan to a particular applicant.
Their goal is to estimate the likelihood of a person defaulting on a loan. This helps them identify individuals who won't default on their loans.
In an ideal world, this firm will get the required information about every single person in the world (e.g. age, income, credit history) and then make the inference on who's going to default. But that's not possible in the real world. In the real world, you can only gather information from a small group of people — say 5,000 — and then use this information to build a model. This model extracts the pattern and quantifies it in a model. In machine learning parlance, this whole process is called "training".
The job of this model is to take in the key input parameters from a new applicant (e.g. age, income, credit history) and make a prediction on whether or not they're going to default.
What's stopping our model from being perfect? What are the sources of error?
The approach of building a machine learning model using labeled dataset is called "supervised learning". Why? Because you're "supervising" the process by providing both the input parameters and the corresponding labels to your machine learning model. The model will then learn how the inputs and the labels are related to each other. You now have a model that represents the relationship between inputs and labels.
This model is only an estimate of the true formula and actually doesn't represent the true formula. To get the true formula, you need to gather information from every single person in the world. That’s obviously not going to happen here. We can only estimate something that’s as close as possible to this true formula.
The difference between our model's prediction and the actual value is called error due to bias.
Let’s call this 'X'. We want this to be as low as possible. It means that our prediction needs to be as close as possible to the real value.
What if we conduct this experiment with a different set of 5,000 people?
Let’s say we repeat the above experiment with a different set of 5,000 people and build a new model. Now this new model is going to predict the likelihood of default using the input parameters. This model will have an error due to bias as well. Let’s call it 'Y'. X won't be equal to Y.
Now go ahead and repeat the experiment a bunch of times with different sets of 5,000 people. You'll see how the error values fluctuate. If everything is perfect, the predictions shouldn't fluctuate.
If they fluctuate too much, then the model depends way too much on what set of 5,000 people we choose for training. It's not a good model because it won't generalize well to new people. If all the above predictions are close to each other, then we can say that the variance is low.
This spread in values is called "error due to variance". It measures how sensitive the model is to variations in the training data.
Bear in mind that they can be close to each other, but still be collectively far away from the true value. In an ideal world, we want the both the errors — error due to bias and the error due to variance — to be low.
This means:
We want the output values as close as possible to the true value, which demonstrates accuracy.
We want those output values to be close to each other, which demonstrates consistency.
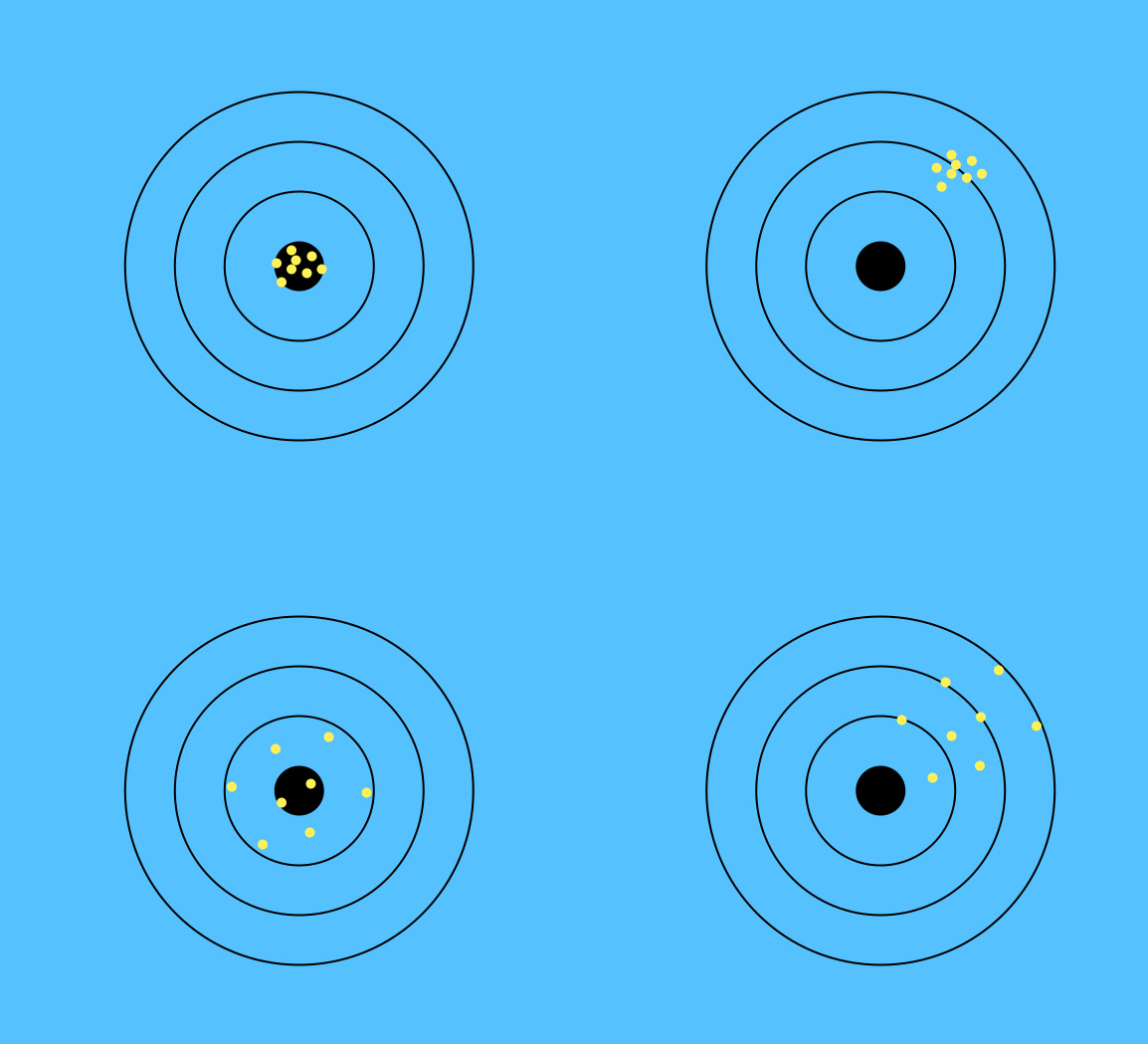
The above diagram represents the concept of bias and variance in machine learning.
Top left: The points are close to the target, which indicates low bias. They are tightly knit as well, which indicates low variance.
Top right: The points are far away from the target, which indicates high bias. But they are tightly knit, which indicates low variance.
Bottom left: The points are close to the target, which indicates low bias. But they are not tightly knit, which indicates high variance.
Bottom right: The points are far away from the target, which indicates high bias. And they are not tightly knit either, which indicates high variance.
When you're working on a machine learning problem in real life, we won't know where the real bull's eye is located. In lieu of that, we create a bull's eye using a finite dataset (e.g. 5,000 people) and build our model hoping that the real bull’s eye would be somewhere close. Training our machine learning model is like calibrating a bow and arrow to hit this target.
Where do we go from here?
Bias vs variance is a game of tradeoff. This tradeoff usually applies to all supervised learning problems e.g. classification, regression. A good model should capture the patterns in our training data and be able to generalize to new data as well. We want low bias and low variance in our machine learning model, but it’s difficult to achieve.
Bias vs variance analysis is a way of understanding our algorithm's ability to generalize. Using this analysis, we can get an estimate of our algorithm's expected generalization error. It's an attempt to find an answer to questions like "Will my algorithm be accurate when making predictions on unknown data?" and "Will my algorithm be consistent across different types of training datasets?".
🔥 Featured job opportunities
Check out Infinite AI Job Board for the latest job opportunities in AI. It features a list of open roles in Machine Learning, Data Science, Computer Vision, and NLP at startups and big tech.
💁🏻♀️ 💁🏻♂️ How would you rate this week’s newsletter?
You can rate this newsletter to let me know what you think. Your feedback will help make it better.